1. Motivación
2. Notación Vectorial
3. Sistemas Lineales Homogéneos
4. Sistemas Lineales Homogeneices
1. Motivación
Cuando consideramos la evolución de sistemas con varios grados de libertad o con varias partículas, natural
mente arribamos al tratamiento de sistemas de ecuaciones diferenciales. En estos sistemas encontramos varias
variables dependientes de una sola variable independiente. El mas natural de los ejemplos es el caso de un sistema
de partículas que se mueve en el espacio bajo la acción de fuerzas externas:
donde, la función F~i = Pj F~
i j expresa la sumatoria de fuerzas externas sobre cada partícula, vale decir:
Pero igual de importante es la posibilidad de convertir una ecuación diferencial ordinaria de orden superior
haciendo el siguiente cambio variable
en un sistema de ecuaciones diferenciales
que puede ser generalizado a:
Notación Vectorial
El sistema lineal antes mencionado
puede condensarse en la siguiente ecuación matricial
u = P (t) u + g (t)
en la cual estamos representando:
Sistemas Lineales Homogéneos
Dado un sistema de ecuaciones diferenciales con coeficientes constantes de la forma _x = A x procedemos de manera análoga al caso de una sola ecuación con coeficientes constantes
con a; aij ; »m constantes. Al sustituir las solución x = » er t
en la ecuación _x = A x obtenemos » r e
r t = » e
por lo cual, el problema se reduce a la búsqueda de los autovalores y autovectores del sistema A x = r »
Sistemas Lineales homogéneos
Todo operador lineal hermético A : V ¡! V;con n autovectores distintos, definidos por A uj i = j ju,
tiene una representación matricial diagonal A^
ij=¸i±ij mediante una transformación de similaridad TAT
A^ con T una matriz unitaria T¡1 = Tz que trasforma la base de A a la base donde A^ es diagonal
auto valores distintos, tiene n autovectores linealmente independientes
los cuales forman base de V y en la cual la representación matricial del
A es diagonal. Pero como siempre es posible pasar de A no diagonal a A^
a diagonal
con los mismos autovalores mediante una transformación de similidaridad TAT
= A^ queda demostrado.
Nos queda determinar la forma de la matriz unitaria de transformación T: Para ello seleccionamos la base
canónica como base de partida de A con:
y la base de autovectores en la cual A^ es diagonal. Por lo tanto T es
la matriz de transformación de una base a la otra, identidad cuando
columna a columna nos damos cuenta que las columnas de
la matriz T son los autovectores de A
donde hemos denotado u (m) i , la componente m del vector j Por lo tanto,
si los n autovalores y autovectores de A son distintos y conocidos, A se dice diagonalizable. Si A es hermética, T¡1 = Tz
y es muy fácil construir la inversa de la matriz de transformacion T: Si los autovalores de A con
degenerados, vale decir si el numero de autovectores linealmente
independientes es menor que n, entonces A no es diagonalmente y no
existe una matriz de transformacion T (T no tiene inversa) tal que TAT
¡1 = A^ :
Pagina de Internet:
http://webdelprofesor.ula.ve/ciencias/nunez/cursos/MetodosMatematicos2/M2ClsSistEcDif.pdf




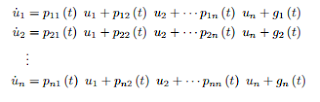





No hay comentarios:
Publicar un comentario